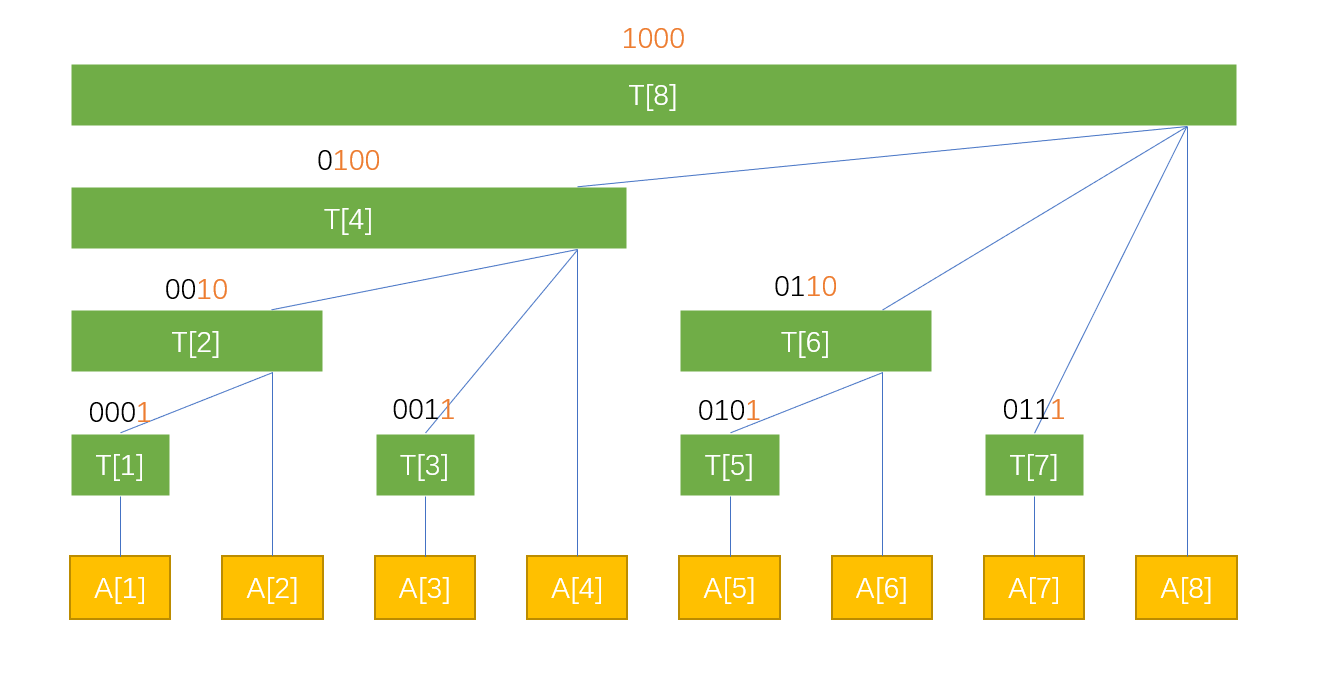
树状数组-优雅的前缀和

基础知识

树状数组中的节点储存的是一定范围之内的和 ，其中节点范围可以参考下面这个图片。绿色为树状数组的节点，黄色为数组的节点。

在使用平常方法时，如果需要频繁查询某个区间的和，那么一般情况下是直接循环累加或者使用前缀和。但是如果数字可以修改呢，例如数字的修改，新增，此时不仅仅要修改数字，还要修改前缀和数组，此时复杂度为O(n)。但是如果利用树状数组，那么我们就不需要全部修改后面所有的数组，只需要修改部分就可以了，树状数组修改的复杂度为O(log n)。

bit1

详细知识

树状数组储存的区间范围为以当前下标开始，向左推移 最后一个1与后面所有的0 所有的范围。

用一个例子来解释：

比如上面树状数组的节点T[6]，6转化为2进制为(0110)，那么 最后一个1与后面所有的0 为(10)转化为10进制为2，那么T[6]所储存的便是A[6]与A[5]的和；同理T[8]储存的是A[1]到A[8]的和。

利用这个方法，如果想知道A[1]-A[7]的和，那么我们只需要知道T[7],T[6],T[4]即可，因为他们分别储存了A[7], A[6]-A[5],A[4]-A[1]的和。注意，7(0111)拆掉最后一个1之后为6(0110)，再拆掉最后一个1为4(0100)，再拆就为0(0000)了。

可以发现，如果我们想知道A的前缀和sum[k]，那么我们只需要将这个k每次拆掉最后一个1，然后在树状数组中去寻找T[k]累加即可。时间复杂度为O(log n)。

如果想要修改某个数字，那么我们只需要知道哪些节点储存了当前节点的值即可。观察上图，反过来加即可。

lowbit

那么就涉及到一个问题，怎么才能快速的把7拆开呢。那么就要引入 lowbit函数 ， lowbit函数 的产生其实与树状数组没有太大的关系，但是他可以高效的解决树状数组的问题。

1
2
3
int lowbit(int x){
	return x & (-x);
}

如果要理解 lowbit ，那么需要先知道数字是怎么用二进制来存储的。正数不用说，重要的是负数。

负数在计算机中是用补码来储存的，补码为正数所对应的二进制 取反后加一 。

例如-1，他是由1(0001)取反后(1110)加一(1111)。所以-1在二进制中存储为(1111)。-6在二进制中储存为(1010)，6在二进制中储存为(0110)，他们只有 最后一个1及后面所有的0是相同的 ，然后再取 与 ，就得到了 最后一个1及后面所有的0 。这样就可以将数字拆分了。

1
2
3
4
5
6
7
int query(int k){
	int sum = 0;
	for(int i = k;i;i -= lowbit(i)){
		sum+=T[i];
	}
	return sum;
}

区间查询

bit1

如上个例子所说，我们要查找前7个数的和，sum[7] = T[7] + T[6] + T[4]。而且我们可以发现6 = 7 - lowbit(7)，4 = 6 - lowbit(6)，而且4 - lowbit(4)刚好等于0，就可以作为循环结束，于是我们只需要一个循环依次来减去他的lowbit即可得到拆分后的序列，然后相加即可。妙哉妙哉！

1
2
3
4
5
6
7
int add(int x){
    int sum = 0;
    for(int i = x;i;i -= lowbit(i)){
        sum += T[i];
    }
    return sum;
}

如果说对于某个区间的求和，利用前缀和的思想，对左节点和右节点依次求和，然后相减，over。

1
2
3
4
5
6
7
8
9
10
11
int add(int l, int r){
	int sum1 = 0;
    int sum2 = 0;
    for(int i = l-1;i;i -= lowbit(i)){
        sum1 += T[i];
    }
    for(int i = r;i;i = lowbit(i)){
        sum2 += T[i];
    }
    return sum2 - sum1;
}

单点修改

对于某个数字要修改的话，我们需要找到其父亲节点一起修改。

bit1

还是用这个图，如果我们要修改A[3]的值，那么T[3]，T[4]，T[8]都要修改。那么怎么从3得到4和8呢，万能的lowbit又登场辣。

仔细观察可以发现，4 = 3 + lowbit(3)， 8 = 4 + lowbit(4)，一直到超出范围再停止，妙蛙，一个循环又搞定了。

1
2
3
4
5
void change(int x, int k){
    for(int i = x;i <= n;i += lowbit(i)){
        T[i] += k;
    }
}

区间修改，单点查询

区间修改没法了，如果一个一个修改这就太麻烦了，那就买个挂吧，对于区间修改特别是多次的区间修改，最容易想到的就是差分。那么ok，那我们就创建一个差分的树状数组呗，这不就搞定了吗。

1
2
3
4
5
6
7
void update(int pos, int k){
    for(int i = pos;i <= n;i+=lowbit(i)){
        c[i] += k;
    }
}
update(l, k);
update(r+1, -k);

然后再对差分数组求和就可以得到答案了，差分数组的特点嘛。

1
2
3
4
5
6
int add(int pos){
	int sum = 0;
	for(int i = pos; i; i-= lowbit(i)){
		sum += c[i];
	}
}

区间修改，区间查询

同样是利用差分，推个公式，利用两个树状数组维护即可，先挖坑了。

建立树状数组

说半天发现没有说怎么建立T数组。

建立树状数组可以将看作元素为0的单点修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
void change(int x, int k){
    for(int i = x;i <= n;i+=lowbit(i)){
        T[i] += k;
    }
}
int main(void){
    ......
    for(int i = 1;i <= n;i++){
        cin>>a[i];
        change(i, a[i]);
    }
    ......
}

over!

线段树

线段树和树状数组一样，他储存的是原数组中某个区间的信息，但是他比树状数组更加全能，用树状数组能实现的基本上都能用线段树来实现，反之则不一定成立，但是树状数组的常数比线段树小。

只要是某个大区间的信息能够由两个更小区间的信息合并而来，那么就可以用线段树来进行处理。

pic1

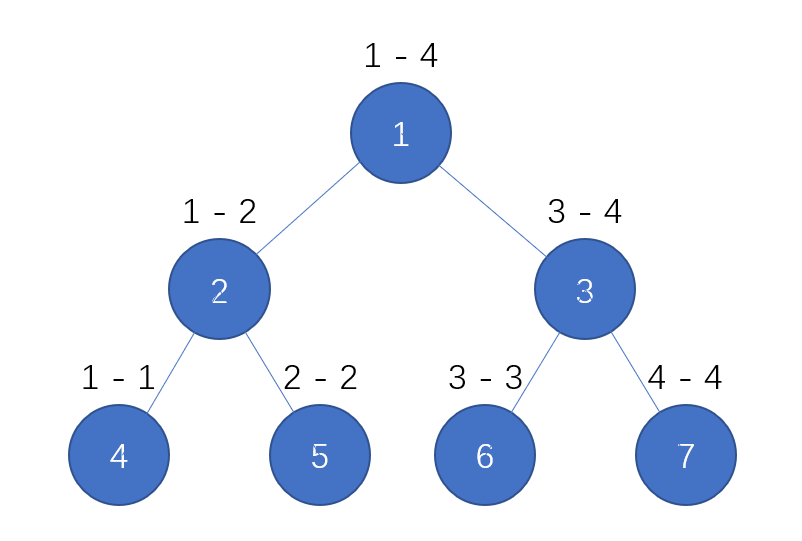
基础知识

观察上图，这就是一颗很普通的线段树，其中1号节点储存的是原数组中1-4的信息，2号存储1-2的信息，4号储存1-1的信息。如果我们想知道1-2的信息，那么我们可以由1-1 ， 2-2的信息合并而来，同理，如果我们想知道1-3的信息，那么我们可以用1-2 ， 3-3的信息合并起来。而且我们在预处理的时候就能够将1-2的信息给处理出来，这样就可以直接使用处理好的信息。

如果我们想修改某个区间的信息，例如2-2的信息，那么我们只需要修改5，2，1三个节点的数据即可。

查询的时间复杂度为O(log n) ，修改的复杂度为O(log n)。

详细知识

代码例题

对于此题，每个节点需要储存的信息为，节点左边界，右边界，区间和

1
2
3
4
5
6
const int maxn = 1e5+5;
struct node{
	int l, r;
	long long sum;
}tree[maxn * 4]; // 线段树一般开4倍空间
long long a[maxn];//原数组

开点建树

利用数组来模拟树，以p*2为左节点，p*2+1为右节点，每个节点处理一半的信息。注意当当前区间左节点与右节点相同时，代表已经到达了叶子节点，此时的信息可以从数组中直接得到。由于递归，当左右两颗树都建好了，那么左右两颗树的信息也都处理好了，此时就能够由两颗树直接处理。时间复杂度为O(nlogn) 。详细看代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*
p: 当前节点编号
l: 当前节点左边界
r: 当前节点右边界
*/
void build(int p, int l, int r){
	tree[p].l = l;
	tree[p].r = r;
	if(l == r){//到了最下方的节点，此时节点直接对应数组
		tree[p].sum = a[l]; // l-l的和就是a[l]，因为只有一个节点，其他情况自由发挥
		return;
	}
	int mid = (l + r) / 2; //将当前区间分割成两个小区间
	build(p*2, l, mid);
	build(p*2+1, mid + 1, r);
	tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 大区间的和为两个小区间的和之和c
}

查询

题目中的操作2，如果我们想知道 [l,r] 的和，那么我们直接去线段树中去寻找即可，注意区间的划分，详细看代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
/*
p: 当前节点
l: 目标区间左端点
r: 目标区间右端点
*/
long long query(int p, int l, int r){
	if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum; // 当前节点所存储的区间在目标区间之内，那么我们直接用当前节点的信息即可
	int mid = (tree[p].l + tree[p].r) / 2; // 注意是将当前区间分割成两半
	long long sum = 0;
	if(mid >= l)  sum += query(p*2, l, r); // 如果有部分目标区间在当前区间所划分的左区间之内，那么去左区间瞅瞅
	if(mid+1 <= r) sum += query(p*2+1, l, r); // 如果有部分目标区间在当前区间所划分的右区间之内，那么去右区间瞅瞅
	return sum;
}

至此，操作2已经完成，即线段树的查询已经结束。接下来是更新的内容了。

更新

先来常规更新

常规更新

与查询类似，如果要更新某个区间的值，那么我们只需要不断的去寻找这个区间，把最下面的节点更改掉，然后更新一下节点的和即可。注意此时的复杂度为O(n log n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/*
p: 当前节点
l: 目标区间左端点
r: 目标区间右端点
k: 增加的数
*/
int update(int p, int l, int r, long long k){
	if(tree[p].l == tree[p].r){ // 到达叶子节点
		tree[p].sum += k; // 区间增加分解到点增加
		return;
	}
	int mid = (tree[p].l + tree[p].r) / 2;
	if(mid >= l) update(p*2, l, r, k); // 如果有部分目标区间在当前区间所划分的左区间之内，那么去左区间改改
	if(mid + 1 <= r) update(p*2+1, l, r, k); // 如果有部分目标区间在当前区间所划分的右区间之内，那么去右区间改改。
	tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 更新当前区间新的和
}

可以发现，这样看起来虽然很高级，但是也有点傻。线段树他是储存的区间信息，那么我们可不可以先把区间处理了，小区间先放一放，等后面要用小区间的信息了再去处理，这样是不是会快一些。此时，我们引入懒标记 。

懒标记

懒标记是对区间是否应该修改进行标记。是否应该修改，应该怎么修改，应该修改多少等等等等，这些都能用懒标记来进行懒处理。

懒标记主要体现在一个懒字，正如上文所说，我们可以先不处理小区间的信息，先处理大区间的信息，把小区间需要处理标记一下，等下次要用这个小区间了，再来处理这个小区间。说起来有点抽象，下面用代码来解释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
long long mark[maxn * 4]; // 懒标记是对线段树节点进行懒标记
void pushdown(int p){
    if(mark[p] != 0){ // 如果存在懒标记
        int l = tree[p].l, r = tree[p].r;
        int mid = (l + r) / 2;
        mark[p*2] += mark[p]; // 懒标记往下传
        mark[p*2+1] += mark[p];
        tree[p*2].sum += (mid - l + 1) * mark[p]; // 区间增加相同的数，即区间和增加 数字*数量
        tree[p*2+1].sum += (r - (mid+1) + 1) * mark[p];
        mark[p] = 0; // 清楚当前节点的懒标记
    }
}
int update(int p, int l, int r, long long k){
    if(tree[p].l >= l && tree[p].r <= r){
        tree[p].sum += (tree[p].r - tree[p].l + 1) * k;
        mark[p] += k;
        return;
    }
    pushdown(p);// 把当前节点的懒标记传下去
    int mid = (tree[p].l + tree[p].r) / 2;
    if(mid >= l) update(p*2, l, r, k);
    if(mid + 1 <= r) update(p*2+1, l, r, k);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum;
}
long long query(int p, int l, int r){
	if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum;
    pushdown(p); // 注意懒标记
	int mid = (tree[p].l + tree[p].r) / 2;
	long long sum = 0;
	if(mid >= l)  sum += query(p*2, l, r);
	if(mid+1 <= r) sum += query(p*2+1, l, r);
	return sum;
}

注意建树，修改，查询时，都是从最大的节点，即1号节点开始走。

例题完整代码

下面给出题目完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<iostream>
using namespace std;
const int maxn = 1e5+5;
struct node{
	int l, r;
	long long sum;
}tree[maxn * 4]; // 线段树一般开4倍空间
long long a[maxn], mark[maxn * 4];
void build(int p, int l, int r){
	tree[p].l = l;
	tree[p].r = r;
	if(l == r){//到了最下方的节点，此时节点直接对应数组
		tree[p].sum = a[l]; // l-l的和就是a[l]，因为只有一个节点，其他情况自由发挥
		return;
	}
	int mid = (l + r) / 2; //将当前区间分割成两个小区间
	build(p*2, l, mid);
	build(p*2+1, mid + 1, r);
	tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 大区间的和为两个小区间的和之和c
}
void pushdown(int p){
    if(mark[p] != 0){ // 如果存在懒标记
        int l = tree[p].l, r = tree[p].r;
        int mid = (l + r) / 2;
        mark[p*2] += mark[p]; // 懒标记往下传
        mark[p*2+1] += mark[p];
        tree[p*2].sum += (mid - l + 1) * mark[p]; // 区间增加相同的数，即区间和增加 数字*数量
        tree[p*2+1].sum += (r - (mid+1) + 1) * mark[p];
        mark[p] = 0; // 清楚当前节点的懒标记
    }
}
void update(int p, int l, int r, long long k){
    if(tree[p].l >= l && tree[p].r <= r){
        tree[p].sum += (tree[p].r - tree[p].l + 1) * k;
        mark[p] += k;
        return;
    }
    pushdown(p);// 把当前节点的懒标记传下去
    int mid = (tree[p].l + tree[p].r) / 2;
    if(mid >= l) update(p*2, l, r, k);
    if(mid + 1 <= r) update(p*2+1, l, r, k);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum;
}
long long query(int p, int l, int r){
	if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum;
    pushdown(p); // 注意懒标记
	int mid = (tree[p].l + tree[p].r) / 2;
	long long sum = 0;
	if(mid >= l)  sum += query(p*2, l, r);
	if(mid+1 <= r) sum += query(p*2+1, l, r);
	return sum;
}
int main(void){
    int n, m;
    cin>>n>>m;
    for(int i = 1;i <= n;i++) cin>>a[i];
    build(1, 1, n);
    for(int i = 0;i < m;i++){
        int ch;
        cin>>ch;
        if(ch == 2){
            int l, r;
            cin>>l>>r;
            cout<<query(1, l, r)<<endl;
        }else{
            int l, r, k;
            cin>>l>>r>>k;
            update(1, l, r, k);
        }
    }
    return 0;
}

至此，线段树解释完毕。

主席树

先拜谢AgOH大佬带我主席树入门，巨巨的教程比我详细多了，我这里没看懂的可以去他哪里看。此处仅讲不修改权值的主席树。

基础知识

主席树最初是用来解决区间第k大问题的，P3834 【模板】主席树，但是用一般的方法，先将区间弄出来，排序，然后再来找肯定会超时，据说是黄嘉泰黄佬最早使用了主席树这个数据结构解决这个问题，为啥叫主席，黄嘉泰（HJT），你品，你细品，啥也不敢想啥也不敢说。

主席树也叫可优化式权值线段树，函数式线段树，函数式，也就是说这个线段树是可以进行拼合与拆解的，将线段树拆分成了无数个小的线段树。

但是如果每个线段树都要一一储存下来，这肯定会爆内存，于是呢，可以简化一下，仅仅储存以当前节点为根节点的左儿子，右儿子，数量。然后儿子又有儿子，无限套娃下去，树就出来辣。之后再来无限套娃，每个状态的树都能出来辣。又因为主席树是可以拆分的，类似于前缀和，就可以得到处于某个区间的状态的树。然后再来找第k大就很简单了。

详细知识

离散化

首先第一步需要对数据进行离散化，所谓离散化其实就是将大化小，仅保留重要的信息，对于处理主席树的问题，最重要的是数字的大小关系，其数值本身其实并不重要，我们只需要知道数字的大小关系，然后在关系表中去查，即可找到其真实数字。

比如对于模板题中的数据，

25957 6405 15770 26287 26465

我们可以仅保留大小关系，离散化为

3 1 2 4 5

这样我们的节点数量就大大减少。然后从后面得到了节点编号后，也可以通过关系再返回原数据。

贴代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<vector>
vector<int> v;
//此处为由普通数据得到离散化后的数据，即25957 -> 3
int getid(int num){
    //二分查找数据，然后可以得到数据再其中的位置
    //二者择一即可
    return lower_bound(v.begin(), v.eng(), num) - v.begin + 1; //巨巨常用方法
    return upper_bound(v.begin(), v.end(), num) - 1 - v.begin() + 1;//我目前使用的方法
}

int main(void){
    ......
	//此处为离散化过程
    //将数据放入vector容器
    for(int i = 1;i <= n;i++){
        cin>>num[i];
        v.push_back(num[i]);
    }
    //将vector容器中所有数据排序
    sort(v.begin(), v.end());
    //去重，unique函数将所有重复数据放到末尾，然后返回非重复数据的最后一个，
    //之后利用earse将末尾的重复数据删除，即得到全部数据的序列，序列包含了数据的大小信息与数据
    v.earse(unique(v.bigin(), v.end()), v.end());
    //离散化完成
    ......
}

此处详细解释v.earse(unique(v.begin(), v.end()), v.end) 与 upper_bound()

earse

unique函数会将范围中的所有重复数据放到序列的末尾，并且返回非重复数据末尾的迭代器。

比如对于1 2 2 4 4 5 ，经过此函数之后会变成1 2 4 5 2 4，然后返回第二个2 的位置，使用earse擦除掉从此处到整个数据结尾的数据，最后就会得到1 2 4 5，就达到完全去重的目的辣。

upper_bound与lower_bound

现在大多数教程包括巨巨的教程其实都用的lower_bound ，但是我再做题的过程中发现有奇怪的地方，因此我更建议用 upper_bound ，如果有容易出现错误的地方请各路大佬指正。

lower_bound 是在区间中查找大于等于某个数的位置，返回一个迭代器。这就涉及到一个问题，如果再后续查点的时候，点并不在初始化的数据之中就会非常麻烦。

比如再 1 2 4 5 中用lower_bound() 查找2与3 ，理论上应该都是查出来2 ，但是在实际情况中，查找出来却是2 与 3，因为一个刚好等于不需要向右偏移，而一个是大于需要偏移，就有点小麻烦，要再处理。

upper_bound 是在区间中查找大于某个数的位置，返回位置的迭代器。

如果使用 upper_bound() ，都让他向右偏移一个位置，然后再减回来，这样就是正确位置，就不需要在处理。

博主在 Super Mario 发现此方法。

此处仁者见仁智者见智。

开点建树

先上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
struct Node{
    int l;//左儿子
    int r;//右儿子
    int sum;//当前节点所含有的数量
}hjt[maxn * 20];//主席树数组
int cnt, root[maxn];
void insert(int l, int r, int pre, int &now, int p){
    hjt[++cnt] = hjt[pre];//将原树复制一份
    now = cnt;//更新当前节点编号，顺便让上一个节点只想当前节点（引用）
    hjt[now].sum++;//节点sum++
    if(l == r) return;//终止条件
    int mid = (l + r) >> 1;
    if(p <= mid){
        insert(l, mid, hjt[pre].l, hjt[now].l, p);//往左收敛，与原树的左儿子为模板，创建当前节点的左儿子
    }else{
        insert(mid + 1, r, hjt[pre].r, hjt[now].r, p);
    }
}
int main(void){
    ......
    for(int i = 1;i <= n;i++){
        insert(1, n, root[i-1], root[i], getid(num[i]));//传入的是离散化之后的数据并不是原数据
    }
    ......
}

这里会传入pre，也就是前模板，然后将前模板复制一次作为当前树节点，当前节点的sum++ ，这样的话，每个同一位置的相同不同节点，除了sum值每次加一，改变了的儿子就会新建一个节点去连接，剩下的那个儿子是不改变的，使用的是原来已经创建好的节点，就达到了节省空间的目的。

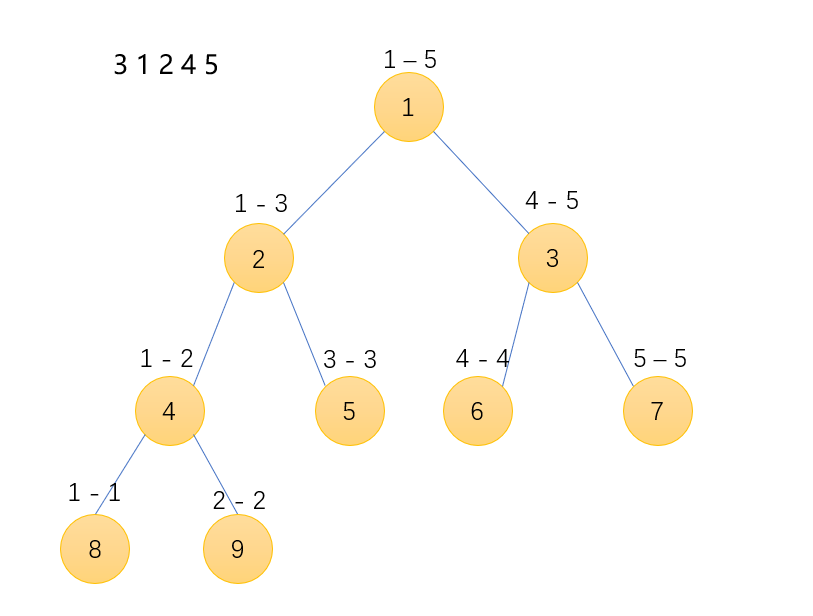
image-1

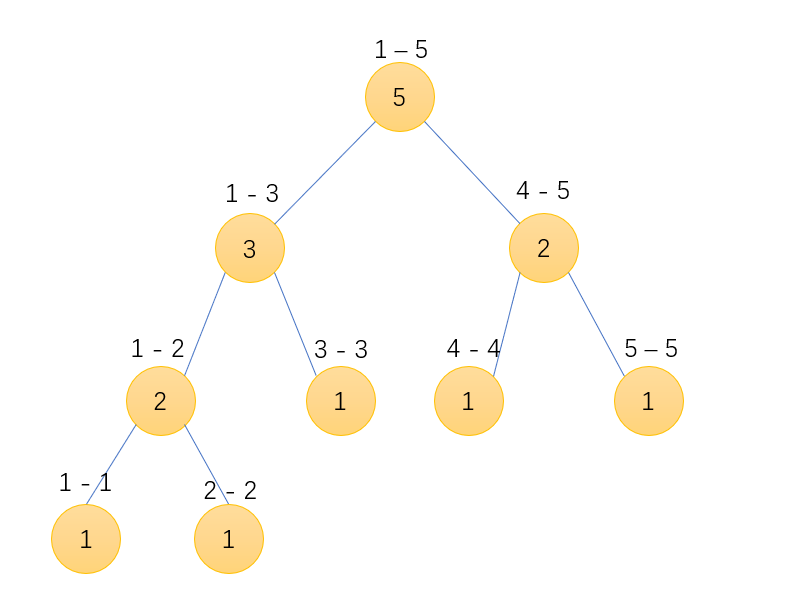
来举个栗子，对于上图3 1 2 4 5 序列，树的编号看作①-⑨，其实是没有编号的，没有任何意义，仅仅是为了方便演示。

第一步3进树，此时位于①号节点，原模板pre = root[0] = 0，hjt[++cnt] = hjt[pre] 之后cnt = 1，hjt[1] 以hjt[0]复制了一份，l = 0, r = 0, sum = 0 。now = cnt，由于引用，root[1] = now = 1。hjt[now].sum++ = 1 。

二分之后，进入②号节点，原模板pre = 上一个节点的原模板的左节点 = hjt[0].l = 0，hjt[++cnt] = hjt[pre] 之后cnt = 2， hjt[2] 以 hjt[0] 复制一份，l = 0， r = 0, sum = 0。now = cnt，由于引用，上一个节点的左儿子发生改变，hjt[1].l = now = 2。hjt[1].l = 2, hjt[1].r = 0，hjt[2].l = 0, hjt[r] = 0，1号节点与2号节点连接成功。hjt[now].sum++ = 1。

二分之后，进入⑤号节点，原模板pre = 上一个节点的原模版的右节点 = hjt[0].r = 0，hjt[++cnt] = hjt[pre]之后cnt = 3，hjt[3]以hjt[0]复制一份，l = 0, r = 0, sum = 0。now = cnt，由于引用，上一个节点的右儿子发生改变，hjt[2].r = now = 3。hjt[1].l = 2, hjt[1].r = 0， hjt[2].l = 0, hjt[2].r = 3， hjt[3].l = 0, hjt[3].r = 0，1号节点与2号节点与三号节点连接成功，即①，②，⑤连接成功，3进入的状态的树建立成功。hjt[now].sum++ = 1。

第二步1进树，此时位于①号节点，原模版pre = root[1] = 1，hjt[++cnt] = hjt[pre]之后cnt = 4，hjt[4] 以 hjt[1] 复制一份，l = 2, r= 0, sum = 1。now = cnt， 由于引用，root[2] = now = 4。hjt[now].sum++ = 2。

二分之后，进入②号节点，原模板pre = 上一个节点的原模板的左节点 = hjt[1].l = 2，hjt[++cnt] = hjt[pre]之后cnt = 5，hjt[5] 以hjt[2]复制了一份l = 0, r= 3, sum = 1。now = cnt 由与引用，上一个节点的左儿子发生变化，hjt[4].l = now = 5，hjt[4].l = 5, hjt[4].r = 0，hjt[5].l = 0，hjt[5].r = 3。hjt[now].sum++ = 2，4号与5号连接成功，并且5号与3号也是连接起来的，这就相当于在原来的基础上多创建了一个分支！！！这就是线段树的精髓所在。

二分之后，进入④号节点，原模版pre = 上一个节点的原模版的左节点 = hjt[2].l = 0，hjt[++cnt] = hjt[pre]之后cnt = 6，hjt[6]以hjt[0]复制一份，l = 0, r = 0, sum = 0。now = cnt，由于引用，上一个节点的左儿子发生变化，hjt[5].l = now = 6。hjt[4].l = 5,hjt[4].r = 0, hjt[5].l = 5,hjt[5].r = 3,hjt[6].l = 0,hjt[6].r = 0。hjt[now].sum++ = 1。

后面就不再演示。与上同理。

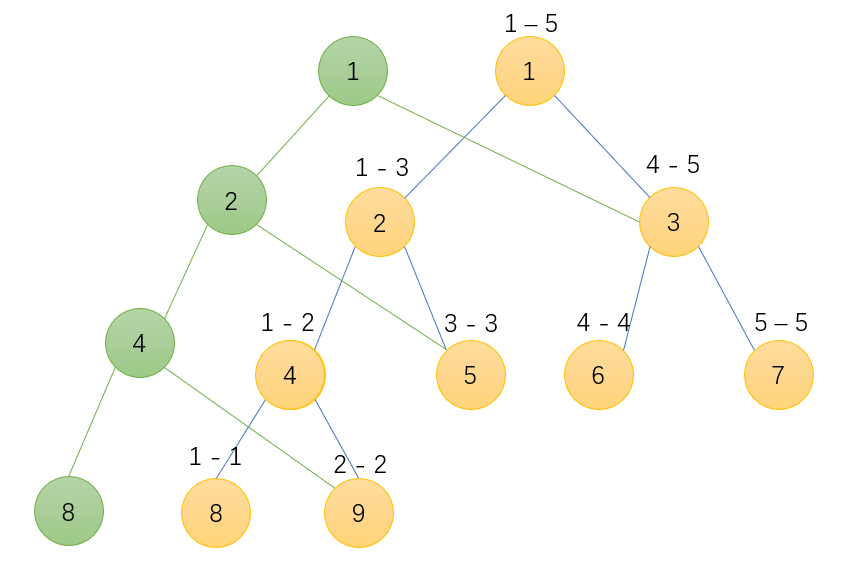
通过演示可以发现，root[1] = 1, root[2] = 4，这其实是每一颗新树的根节点编号。hjt[5].r = 3，可以发现他使用的是原来已经创建好的节点，仅仅去改变需要改变的l分支，就十分的节省空间。也就达到了下面这张图的目的。

image-2

而且我们可以发现一个重要的结论，线段树是可以加减拆分的，例如hjt[root[2]].sum - hjt[root1].sum = 1，表示的是单独1进树的节点数量状态。

例如此为3 1 2 4 5全部入树的状态

image-3

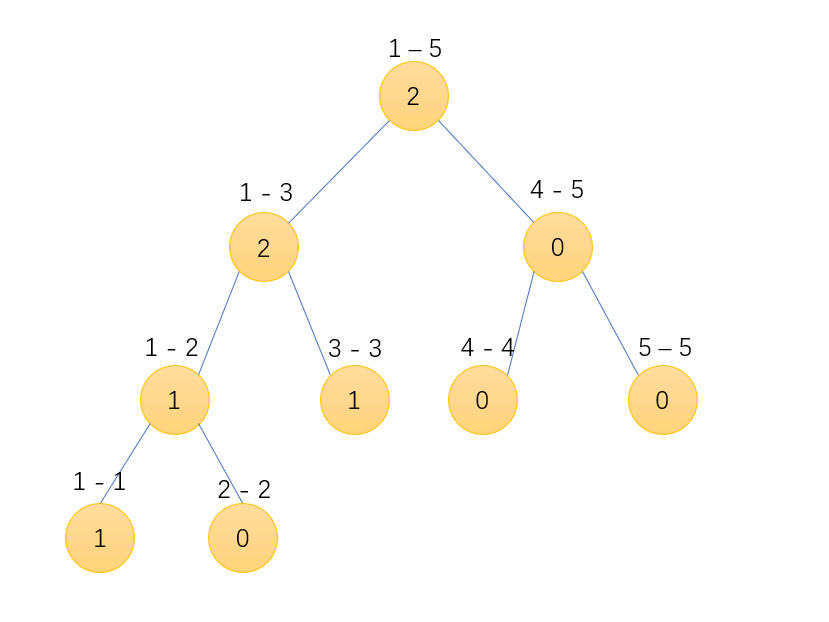
此为3 1入树状态

image-4

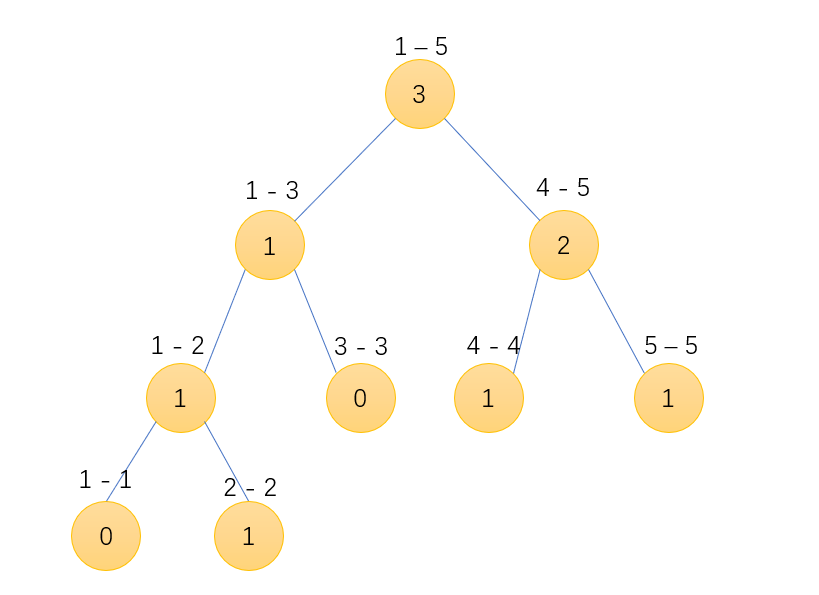
两者相减之后即为2 4 5入树的状态

image-5

所以主席树真的是非常神奇啊！大佬牛逼！！！

查询

上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int query(int l, int r, int L, int R, int k){
    //cout<<l<<r<<endl;
    if(l == r) return l;
    int mid = (l + r) >> 1;
    int temp = hjt[hjt[R].l].sum - hjt[hjt[L].l].sum;//左子树上有多少个数字,外面已经减过1了，这里就不用减1了
    if(k <= temp){
        return query(l, mid, hjt[L].l, hjt[R].l, k);
    }else{
        return query(mid + 1, r, hjt[L].r, hjt[R].r, k - temp);//全部的第k大也就是右边的第k-左大
    }
}
int main(void){
	......
	for(int i = 1;i <= m;i++){
        int l, r, k;
        cin>>l>>r>>k;
        cout<<v[query(1, n, root[l-1], root[r], k) - 1]<<endl;//*
    }
    ......
}

首先，[L,R]应该的从 R 到 L-1，所以应该的root[R]这棵树减去root[L-1]这棵树才是[L,R]这颗树。

然后就是query里面的第二个else，全部范围的第k大应该是右边的第k-左大，比如一共有6个数字，左边3个右边3个，一共的第5大应该的右边的第5 - 3大。

最后，由于最开始是存的离散化之后的数据，需要反引用，又因为编号大小是从1开始的，而数据是从0开始的需要减1。

至此，主席树解释完毕。

模板题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 2e5 + 5;
struct Node{
    int l, r, sum;
}hjt[maxn*40];
int cnt, root[maxn];
int num[maxn];
vector<int> v;

//离散化
int getid(int x){
    return lower_bound(v.begin(),v.end(),x) - v.begin() + 1;
}

//插入
void insert(int l, int r, int pre, int &now, int p){
    hjt[++cnt] = hjt[pre];//将原树复制一份
    now = cnt;
    hjt[now].sum++;
    if(l == r) return;
    int mid = (l + r) >> 1;
    if(p <= mid){
        insert(l, mid, hjt[pre].l, hjt[now].l, p);
    }else{
        insert(mid + 1, r, hjt[pre].r, hjt[now].r, p);
    }
}

//查询
int query(int l, int r, int L, int R, int k){
    if(l == r) return l;
    int mid = (l + r) >> 1;
    int temp = hjt[hjt[R].l].sum - hjt[hjt[L].l].sum;
    if(k <= temp){
        return query(l, mid, hjt[L].l, hjt[R].l, k);
    }else{
        return query(mid + 1, r, hjt[L].r, hjt[R].r, k - temp);
    }
}

int main(void){ 
    int n, m;
    cin>>n>>m;
    for(int i = 1;i <= n;i++){
        cin>>num[i];
        v.push_back(num[i]);
    }
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(),v.end()), v.end());
    for(int i = 1;i <= n;i++){
        insert(1, n, root[i-1], root[i], getid(num[i]));
    }
    for(int i = 1;i <= m;i++){
        int l, r, k;
        cin>>l>>r>>k;
        cout<<v[query(1, n, root[l-1], root[r], k) - 1]<<endl;
    }
    return 0;
}

字典树

基础知识

字典树故名思意就是和字典一样的，一个字母一个字母来查，分流，然后形成一个在O(L)时间内查找到字符串的树形结构，非常非常快，与哈希相比在处理长字符串更有优势，而且随时可以新增。但是空间复杂度巨大无比，典型的空间换时间。O(N*L)，最大字符串数量乘以最大字符串长度。

详细知识

其实字典树就是每个节点有26个儿子节点的树，和以前的差不多，直接上代码了。哦对了，根节点的编号是0，也就是说根节点连的每个字符串的第一个字母。然后就没啥注意点了。

建树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct Node{
    int son[26];
}trie[manx * maxl];
void insert(string str, int id){
	int now = 0;
    int l = str.length();
    for(int i = 0;i < l;i++){
        int ch = str[i] - 'a';
        if(trie[now].son[ch] == 0){
            trie[now].son[ch] == ++cnt;//动态开点
        }
        now = trie[now].son[ch];//层层深入
    }
    root[now] = id;//最后一个位置标记当前字符串的编号
}

对于字符串一个字母代表一层，每过一个字母就要深入一层，如果下一个字母没有就开一个空间给他，走到最后了，该字符串的分支就到了，标记一下就好了。

查询

1
2
3
4
5
6
7
8
9
10
11
12
int search(string str){
	int now = 0;
    int l = str.length();
    for(int i = 0;i < l;i++){
        int ch = str[i] - 'a';
        now = trie[now].son[ch];//层层深入
        if(now == 0){//没有说明以前没有插入这个分支，就不存在咯
            return 0;
        }
    }
    return root[now];//走到最后一层了，把标记的编号输出即可，就是该字符串的编号
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
using namespace std;
const int maxn = 1e5;
struct node{
    int son[26];
}trie[maxn];
int cnt, root[maxn];
void insert(string str, int id){
    int now = 0;
    int l = str.length();
    for(int i = 0;i < l;i++){
        int ch = str[i] - 'a';
        if(trie[now].son[ch] == 0){
            trie[now].son[ch] = ++cnt;//动态开点
        }
        now = trie[now].son[ch];
    }
    root[now] = id;
}
int search(string str){
    int now = 0;
    int l = str.length();
    for(int i = 0;i < l;i++){
        ch = str[i] - 'a';
        now = trie[now].son[ch];
        if(now == 0) return 0;
    }
    return root[now];
}
int main(void){
    int n;
    cin>>n;
    string str;
    for(int i = 1;i <= n;i++){
        cin>>str;
        insert(str,i);
    }
    cin>>n;
    for(int i = 1;i <= n;i++){
        cin>>str;
        cout<<search(str)<<endl;
    }
    return 0;
}

over！

最小生成树

基础知识

最小生成树是图的给你N个节点，M条边，让你在M条边中找N-1条边使N个节点联通，并且权值和最小，当前情况形成的树称为最小生成树。生成最小生成树常用两种方法， 分别是Prim与Kruskal。

Prim在稠密图中比Kruskal优，在稀疏图中比Kruskal劣。

Prim

Prim是对每个点周围找最短的边，然后将这个边怼进去，对这个集合找所连的边的最短边怼进去，重复下去就找到了最小生成树了。

dis[maxn]储存当前集合到其他点的距离，初始化为inf，相当于把当前集合所连边怼进集合，注意取最小值，因为可能有重边。

vis[maxn]用来标记每个点，已经找到的点就标记起来，不用再去找了

tot表示边的数量，数量等于n-1时结束查找

ans表示最后答案，也就是最小树的权值和

用链式前向星储存答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int dis[maxn], vis[maxn], tot, ans;//边集合，边数量，答案
inline void prim(void){
    int now = 1;//从节点1开始
    for(int i = 2;i <= n;i++) dis[i] = inf;//初始化
    for(int i = head[now];i;i = edge[i].next){//将当前节点的所连的所有边放进集合
        dis[edge[i].to] = min(dis[edge[i].to], edge[i].w);
    }
    while(++tot <= n-1){
        vis[now] = 1;
        int min_now = inf;
        for(int i = 1;i <= n;i++){//寻找与当前集合所连边的最小边，注意这里是1到n，当找不到最小值时，原图未连通
            if(!vis[i] && dis[i] < min_now){
                min_now = dis[i];
                now = i;
            }
        }
        ans += min_now;
        for(int i = head[now];i;i = edge[i].next){//将边放进去
            if(!vis[edge[i].to]){//边所连的点已经标记好了就不用放了
                dis[edge[i].to] = min(dis[edge[i].to], edge[i].w);
            }
        }
    }
}

Kruskal

Kruskal与Prim相似，不过Kruskal是将所有边中最小的边一个一个连，然后利用并查集来判断两点是否连接，未连接就用这个较小边来连接，否则就寻找下一个边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline cmp(struct Edge p, struct Edge q){//将所有边按权值从小到大排序
    return p.w < q.w;
}
int ans, tot;
inline void Kruskal(void){
	sort(edge, edge + m,cmp);//这里不需要太在意是否有方向，只需要关注两个节点，因此单向边即可，只有m条边
	for(int i = 0;i < m;i++){
		int rootp = find(edge[i].from);
		int tootq = find(edge[i].to);
		if(rootp == rootq) continue;//如果两个点已经连接，跳过当前边
		id[rootp] = rootq;//连接起来
		ans += edge[i].w;
		if(++tot == n-1) break;//找到n-1条边结束，如果到最后都没有找到n-1条边，说明原图未连通
	}
}

模板

P3366 【模板】最小生成树

Prim

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = 5e3 + 4;
const int maxm = 2e5 + 5;
const int inf = 0x7ffffff;

//链式前向星部分
struct node{
    int to, w, next;
}edge[maxm<<1];//需要遍历一个点的所有边，因此需要双向边
int head[maxn], cnt;
inline void add(int u, int v, int w){
    edge[++cnt].to = v;
    edge[cnt].w = w;
    edge[cnt].next = head[u];
    head[u] = cnt;
}

//Prim部分
int tot, ans, dis[maxn],vis[maxn];//边数，权值和，集合，标记数组
int n, m;
int jd;//判断是否未连通
inline void prim(void){
    int now = 1;//从节点1开始
    for(int i = 2;i <= n;i++){//最开始集合初始化为正无穷，1不用初始化，因为1与1连通  
        dis[i] = inf;
    }
    for(int i = head[now];i;i = edge[i].next){//将与1连通的所有边放进来，min是为了防止有重边
        dis[edge[i].to] = min(dis[edge[i].to], edge[i].w);
    }
    while(++tot <= n-1){
        jd = 0;
        int minn = inf;
        vis[now] = 1;//标记
        for(int i = 1;i <= n;i++){//找到集合里面最小边，注意是1-n
            if(!vis[i] && minn > dis[i]){
                minn = dis[i];
                now = i;
                jd = 1;
            }
        }
        if(!jd) return 0;//如果没有找到最小边，说明未连通
        ans += minn;
        for(int i = head[now];i;i = edge[i].next){//将新点的所有边放进集合
            if(!vis[edge[i].to])
            dis[edge[i].to] = min(dis[edge[i].to], edge[i].w);
        }
    }
}
signed main(void){
    cin>>n>>m;
    for(int i = 0;i < m;i++){
        int u, v, w;
        cin>>u>>v>>w;
        add(u, v, w);//双向边
        add(v, u, w);
    }
    prim();
    if(jd) cout<<ans;
    else cout<<"orz";
    return 0;
}

Kruskal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn = 5e3 + 5;
const int maxm = 4e5 + 5;

//并查集部分
int id[maxn];
inline void init(int n){
    for(int i = 1;i <= n;i++) id[i] = i;
}
inline int find(int p){
    if(p == id[p]) return p;
    return id[p] = find(id[p]);
}

//链式前向星部分
struct edge{
    int from, to, w;   
}edge[maxm];//这里是单向边，不用开两倍
inline int cmp(struct edge p, struct edge q){
    return p.w < q.w;
}

//kruskal部分
int n, m;
int ans, tot;
inline void kruskal(void){
    sort(edge, edge + m, cmp);//排序
    for(int i = 0;i < m;i++){
        int rootp = find(edge[i].from);
        int rootq = find(edge[i].to);
        if(rootq == rootp) continue;//当前边的两点已经连通，跳过
        ans += edge[i].w;//连通
        id[rootq] = rootp;
        if(++tot == n-1) break;//找到n-1条边即可退出
    }
}
signed main(void){
    cin>>n>>m;
    init(n);
    for(int i = 0;i < m;i++){
        cin>>edge[i].from>>edge[i].to>>edge[i].w;//kruskal只用考虑一边的两点，因此单向边足矣
    }
    kruskal();
    if(tot == n-1) cout<<ans;//如果tot不等于n-1说明原图未连通
    else cout<<"orz";
    return 0;
}

over！